Logarithm - The basics

In this blog post, let's break down the basics of logarithms. Logarithms come in handy when dealing with big numbers, providing a convenient way to express them. Usually, these big numbers are the result of exponential growth. Logarithms, acting as the inverse of exponentiation, help us shrink these big numbers into smaller and more manageable ones.

Take the number 1000000000 (10⁹) for instance. If we use logarithms on 10⁹, we get 9. So, in this case, 9 is the simpler way to talk about 10⁹. In other words, 9 is the logarithmic representation of 10^9. 

In a nutshell, logarithms does the inverse of exponentials. This relationship mirrors other mathematical pairs, such as subtraction being the inverse of addition and division being the inverse of multiplication. Exploring these logarithmic basics helps us make sense of dealing with large numbers in a more straightforward way. Being inverse of exponentials, it tells us how many times a number should be raised to produce the given number. It also reduces multiplication into additions and divisions into subtractions. But more on this later.

Exponential and logarithmic forms

Determining logarithms involves using the logarithmic function on an equation expressed in exponential form. Conversely, exponential functions can be applied to logarithmic equations. Let's start by understanding both exponential and logarithmic forms.

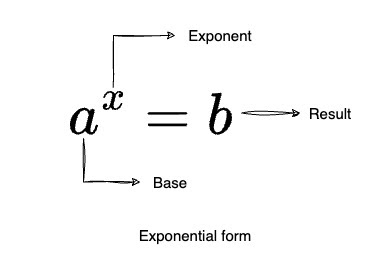
Exponential forms

In exponential form, a base is raised to an exponent. This exponent indicates how many times the base needs to be multiplied to achieve the specified result.

Logarithmic form

In logarithmic form, the log function with a specific base is applied to the result value. This process calculates the exponent, which signifies how many times the base needs to be raised to produce the given result.

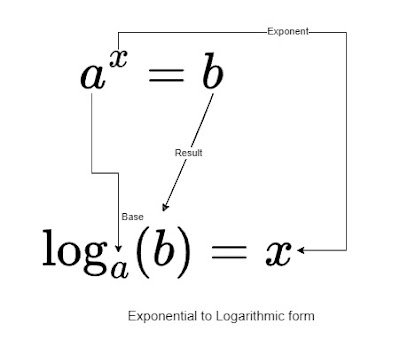
Comparison of the forms

Below is a visual depiction illustrating the inverse relationship between exponential and logarithmic forms.

Calculating with logarithm

There are two types of logarithmic calculation that I will be covering.

• Solving exponential forms with logarithmic function
• Solving logarithmic forms with exponential function

Solving exponential forms with logarithmic function

There are three steps in solving an exponential form using logarithm.

• Step 1: Apply log on both sides
• Step 2: Apply cancellation rule
• Step 3: Using calculator or a log table book, figure out the log value.

Cancellation rule

Before moving to example, let's see what is Cancellation rule. 

In logarithm calculation, the log with base and the base can cancel each other given that both the bases are same number.

In above example, b is the base and it cancels out each other. Applying cancellation rule is something that we should remember. Let us proceed to examples.

Example 1

Let us calculate logarithm for 10^x = 100

Step 1 - Apply log on both sides

Step 2 - Apply cancellation rule

By cancellation rule, log₁₀ and 10 cancel out each other.

Step 3 - Using calculator or a log table book, figure out the log value.

Use a calculator or a log table book. The value of log₁₀(100) will be 2. Therefore, x = 2.

Example 2

Now let us take a little more not-so-easy example. Let us calculate x in 6.5^x = 399.32

Step 1 - Apply log on both sides

Step 2 - Apply cancellation rule

Applying cancellation rule, we are left with the below equation.

Step 3 - Using calculator or a log table book, figure out the log value.

Use a calculator or a log table book. The value of log_6.5(399.32) will be 3.2. Therefore, x = 3.2.

Solving logarithmic form using exponential function

Just as logarithm and exponents are inverse of each other, their calculation methods are also inverse. When solving a logarithmic equation, we utilize the same steps employed in solving exponential equations. However, in this case, we use exponentiation instead of logarithms.

Step 1: Exponentiate both sides with the base

Step 2: Apply cancellation rule

Step 3: Compute the exponential

Cancellation rule

The cancellation rule is inversed as well. Now we cancel the base with the based log given that both bases are the same number.

Example

Let us solve exponential form for the equation log₆(x) = 73.71

Step 1: Exponentiate both sides with the base

Step 2: Apply cancellation rule

After applying the cancellation rule, we get the below equation.

Step 3: Compute the exponential

Compute the exponential equation. Here 6^(2.4) is 73.71

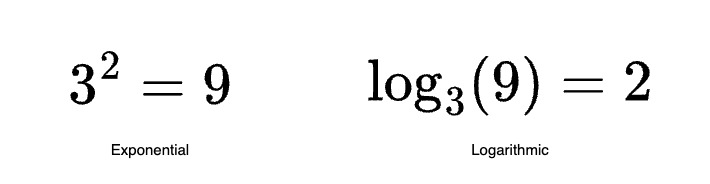
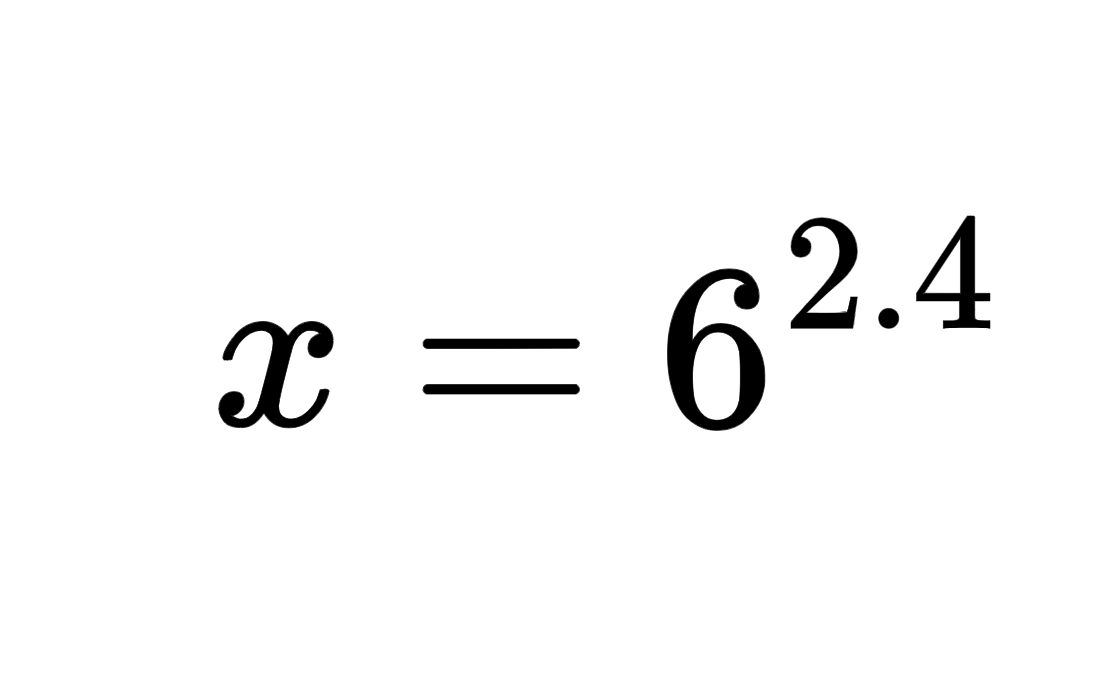
With this, I conclude the basics of logarithms. In upcoming post, I will give some real-time application of logarithms. If you know where logarithms is used in real-time, drop it in the comments.